Esta página quizá resulte un poco difícil para algunos, pero no me es posible hacerlo más fácil. Lo que verán aquí demostrado es de un nivel elemental de primer año de universidad.
En la matemática pitagórica, algunos números eran considerados con cualidades geométricas. Había números cuadrados (2x2=4), oblongos (2x3=6), cúbicos (2x2x2=8), y triangulares (1+2+3+4=10) entre otros. De aquí vienen términos tales como "x al cuadrado" o "x al cubo".
Se le llama número triangular a la suma de números consecutivos del tipo:
Pues al ser dispuestos gráficamente los valores de estos números, forman un triángulo equilátero:
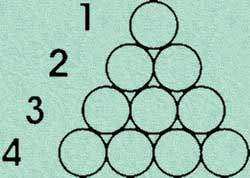
Se dice entonces, que 10 es un número triangular, como resultado de la suma:
10 = 1+2+3+4
Denominaremos a la suma de sus números componentes desarrollo.
En la antigüedad, en oriente,
al desarrollo de un número triangular se le llamaba
la luz del número. Hay que tener en cuenta que la matemática
antigua no era un mero juego de recombinaciones numéricas, desprovisto
de sensibilidad, sino que implicaba paralelos filosóficos y metafísicos,
y era un medio de contemplación y meditación sobre el cosmos.
El número cúbico estaba conformado por el producto del número por sí mismo y por sí mismo: 2x2x2; 4x4x4; n x n x n. Por ejemplo, el número 8 es un número cúbico:
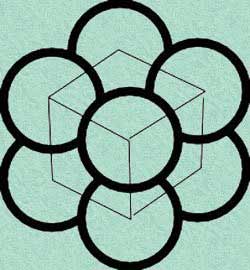
Esto implica que si tomamos 8 esferas las podemos empaquetar cúbicamente, ocupando los vértices del cubo, como ilustra la figura de arriba. Esto puede realizarse con cualquier número de esferas, a condición de que dicho número sea un número cúbico, o lo que es lo mismo: que su raíz cúbica sea exacta (que dé un número entero sin decimales).
En ocasión de estar estudiando algunos pormenores de matemárica oriental, vi de manera instantánea que se cumplía la siguiente igualdad (llamémosle igualdad 1:
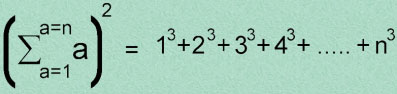
La cual expresa que el cuadrado de un número triangular es igual a la suma de los cubos de cada uno de los números de su desarrollo. Para dar un ejemplo:
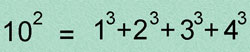
Ignoro si esta proposición ha sido descubierta, quizá ya lo ha sido (háganme saber), por las dudas la demostraré a continuación:
La demostración será inductiva, por tanto debemos ver si se cumple para 1: 1 al cuadrado es igual a 1 al cubo, por tanto se verifica.
El segundo paso es suponer que se cumple para n, que pertenece a los triangulares naturales; y desarrollar la igualdad hasta arribar a otra igualdad ya conocida:
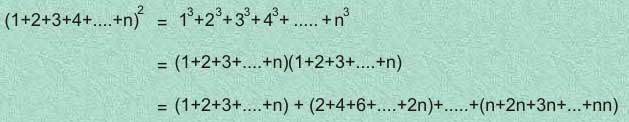
Si se observa la dinámica
de correspondencias entre un número cualesquiera de la primera
igualdad con grupos de números de la segunda igualdad, se verá
que para el
n-simo término de la segunda igualdad (n) se corresponde con el
desarrollo
n-simo:

(n-1). Pues con (n-1) calcularíamos la suma triangular de el número anterior a n.
Por lo tanto, queda demostrado.
La fórmula de este desarrollo es:
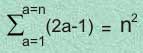
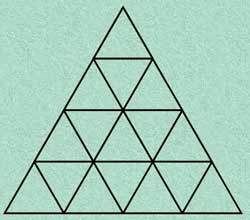
El cual tiene la virtud de llenar
el espacio completamente, a diferencia de las esferas, que dejan espacios
libres. El lector puede verificar que de añadirse más niveles,
la suma del desarrollo siempre admitirá una raíz cuadrada
exacta. Para que quede más claro, en esta pirámide de cuatro
niveles tenemos que:
1+3+5+7 = 16, que equivale a
4 al cuadrado
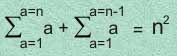
La cual, explicada en romance, quiere decir que la luz de un número n más la suma de la luz de un número (n-1) es igual al cuadrado de n.
Me pregunto si habrá cabida
para el desarrollo de formas poliédricas.
Si alguno lo sabe, bienvenido que lo diga.