Si bien poliedro es un cuerpo tridimensional limitado por caras planas, también es necesario definir previamente los elementos constitutivos sobre los cuales se sustenta, que es la geometría elemental Euclidiana:

Geometría elemental
con definiciones elementales

Dimensión: Es el número de coordenadas imprescindibles para definir un objeto. Se entiende que los ejes de coordenadas son perpendiculares entre sí. Por ejemplo, para definir una línea basta con una sola dimensión, para un triángulo sólo hacen falta dos coordenadas, es decir que se trata de una figura plana, o sea que se ubica en un espacio de 2 dimensiones. Para una pirámide, en cambio, hace falta una coordenada adicional, puesto que es un sólido, o sea que se trata de un espacio de 3 dimensiones. El prefijo 'hiper'dimensional se refiere usualmente a la 4º dimensión y superiores.

Punto: es el objeto adimensional, es decir que tiene 0 dimensiones. Euclides de Alejandría lo definió como "aquello que no tiene partes".

Línea: es el arrastre de un punto en alguna dirección. Puede considerarse que la línea está formada por una sucesión infinita de puntos.Tiene 1 dimensión.

Plano: es el arrastre de una línea fuera de la dimensión en la que yace. Puede considerarse como una sucesión infinita de líneas.Tiene 2 dimensiones.

Espacio: es el arrastre de un plano fuera de las dimensiones en la que yace, es decir en una dirección perpendicular a dicho plano. Puede considerarse como una sucesión infinita de planos. Esto es: un desplazamiento en una tercera dimensión.

Hiperespacio: es el arrastre de un volumen en una dirección tal que está fuera de las 3 dimensiones en las que yace; esto es a lo largo de un cuarto eje de coordenadas perpendicular a los otros tres. Dado que nosotros estamos habituados a una percepción tridimensional, el considerar una dimensión adicional escapa un poco al entendimiento cotidiano, todos los objetos a nuestro alcance son tridimensionales: tienen ancho, alto y profundidad. Aunque puede darse un ejemplo concreto: si consideramos a la línea de tiempo como un eje de coordenadas adicional a los tres del espacio, tenemos el 'desplazamiento' de algo tridimensional a lo largo de una 4º dimensión. Así por ejemplo, con tiempo, podemos contemplar una semilla y percatarnos de su desarrollo (tridimensional) que la hace convertirse en retoño, planta, flor, fruto, semilla nuevamente, y así ad infinitum. Estamos inmersos en el tiempo, y sin embargo se nos escapa de las manos inexorablemente. Como diría Násafi (filósofo persa del siglo XIII) frecuentemente en su Libro del Hombre Perfecto: "Yo coloco el hilo conductor en las manos de los hombres perspicaces para que ellos, mediante la reflexión, lo descubran por sí mismos".

Observación: puede generalizarse que un objeto n-dimensional, siendo 'n' un número natural, siempre estará acotado, limitado por elementos n-1 dimensionales. Por ejemplo: un polígono (2 dimensiones) está limitado por aristas (línas, 1 dimensión); un objeto tridimensional siempre está limitado por planos, es decir por elementos bidimensionales. Este es el caso de los poliedros, los cuales están limitados por caras planas poligonales. En el caso de los politopos, denominación que reciben los cuerpos de 4 dimensiones, están limitados por células, que son volúmenes tridimensionales.

Definición de Polígono

Se llama polígono (del griego poli: muchos; gono: ángulo) a la región del plano delimitada por un número finito de segmentos. Estos segmentos se llaman lados o aristas, y los extremos se llaman ángulos o vértices. Los polígnonos son figuras planas, es decir que sólo tienen dos dimensiones.

Los polígonos son los análogos en el mundo de dos dimensiones, a los poliedros en el mundo tridimensional.

Cada polígono tiene un nombre (de origen griego) el cual se corresponde con la cantidad de ángulos que posee. Así, por ejemplo un polígono de 5 ángulos recibe el nombre de pentágono: penta: cinco; gono: ángulo. Es decir que a todo polígono le corresponde un prefijo griego que establece su número de ángulos, seguido por el sufijo 'gono'. A continación van los nombres griegos correspondientes a cada número:

Puede verse que del 1 a 9 se establecen las unidades que servirán para cualquier decena; siempre la decena como prefijo y la unidad como sujijo, como sucede en nuestro idioma; la excepción serían los números que van del 11 al 19, que reciben nombres propios, tal y como sucede con nuestro idioma con los números 11, 12, 13, 14 y 15. Así, por ejemplo, 21 sería 'icosamono' y un polígono de 21 lados sería entonces un 'icosamonógono'. Lo cual resulta un tanto gracioso. Por último, sería oportuno destacar que del prefijo 'miria' correspondiente a 10.000 se deriva la palabra española miríada, que quiere decir 'cantidad muy grande, e indefinida' según la Real Academia Española.

Categorías de polígonos

Hay varias maneras de categorizar un polígono. Categorizar es ordenar algo en relevancia a alguna cualidad o cualidades. Una de las categorías en que pueden ser ordenados los polígonos es la ya vista, en base a su cantidad de ángulos, es decir que es un ordenamiento en base a la cantidad 'ángulo'.

Otra categoría se puede hacer según las cualidades de sus lados y/o ángulos:

Polígono regular: si todos sus lados y ángulos son iguales.

Polígono semirregular: si todos sus lados son iguales pero no sus ángulos, como por ejemplo el rombo.

Polígono irregular: cuando sus lados y ángulos son desiguales.

Otra categoría corresponde a cierta operación de trazado de líneas en el polígono:

Polígono convexo: se dice que un polígono es convexo si para todo par de puntos que contiene el polígono (sea en su perímetro o en su interior) puede trazarse un segmento quedando éste en todo su tramo dentro del polígono inscripto. Es evidente que para que esto ocurra el ángulo interno de cualquier vértice del polígono debe ser menor a 180º.

Polígono cóncavo: cuando no es convexo, es decir que el segmento, en todo o en parte, queda fuera del perímero del polígono. Por ejemplo, un polígono en forma de estrella, si se intentan unir los vértices del mismo, el segmento inevitablemente pasa por fuera del polígono. Todo polígono que tenga al menos un vértice con un ángulo interno mayor a 180º es cóncavo.

Definición de Poliedro

Habiendo definido al polígono, es posible definir análogamente al poliedro, como:

una porción de espacio tridimensional
delimitado por un número finito de polígonos

Asimismo cada poliedro (del griego poli: muchos; edro: caras) tiene un nombre griego que se corresponde al número de caras que posee y se utiliza la misma nomenclatura anteriormente citada, y será el prefijo (número) más 'edro'. Así por ejemplo un poliedro de 20 caras se llamará 'icosaedro' y uno de 30 caras 'tricontaedro'.

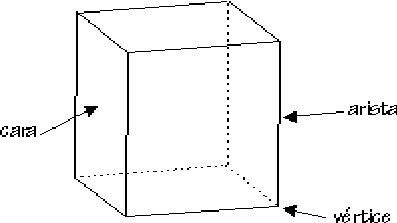
Un poliedro está constituído por polígonos que reciben el nombre de caras, por aristas (que son las líneas en donde se tocan las caras de dos polígonos) y por vértices (que es donde confluyen los vértices de varios polígonos).

Así como hemos visto en los polígonos, los poliedros pueden ser clasificados de muy diversas maneras, siendo las categorías más elementales las que siguen:

Categorías de Poliedros

Poliedros regulares, semirregulares e irregulares

Poliedro regular: cuando sus caras son polígonos regulares. Más específicamente, se dice que es regular si cumple con dos requisitos:

a) Todas las caras son polígonos regulares y dichos polígonos tienen la misma cantidad de lados (cantidad que por convención es llamada p); es decir que las caras del poliedro son todas iguales.

b) En cada vértice del poliedro convergen la misma cantidad de polígonos ( a dicha cantidad se la suele llamar q) . Ver nota

Poliedro semirregular: hay dos clases:

Poliedro semirregular del primer tipo:

a) Todas sus caras son polígonos regulares de dos o tres tipos (por ejemplo, cuadrados y triángulos equiláteros, o también octógonos, exágonos y cuadrados).

b) Cada vértice está rodeado por la misma secuencia de polígonos, son superponibles (es decir cada vértice tiene otro análogo al otro extremo del poliedro, y cara tiene una cara opuesta al otro extremo del poliedro) y yacen sobre el mismo radio de una esfera imaginaria (llamada esfera circunscripta).

c) Sus aristas tienen la misma longitud.

Poliedro semirregular del segundo tipo:

a) Sus caras son polígonos semirregulares y son superponibles.

b) Sus vértices son de dos o tres tipos, esto quiere decir que reúnen dos o tres secuencias diferentes de polígonos.

Poliedro irregular: cuando sus caras son polígonos irregulares.

Poliedros cóncavos y convexos

Poliedro convexo: cuando el segmento que une dos puntos cualesquiera del poliedro queda dentro del poliedro. Puede generalizarse que si un poliedro tiene sus ánglulos diedros menores a 180º es convexo.

Poliedro cóncavo: cuando no es convexo. Algunos o todos sus ángulos diedros son mayores a 180º.

Ambas categorías (regulares, semirregulares e irregulares por un lado y cóncavos y convexos por el otro) son combinables entre sí, lo cual deviene en una gran cantidad de conjuntos, es decir que hay poliedros regulares convexos, regulares cóncavos, semirregulares convexos y semirregulares cóncavos, irregulares convexos e irregulares cóncavos, que a su vez dan origen a nuevos conjuntos de categorías, algunos de ellos están constituídos por un número finito de poliedros y otros por un número infinito. Veamos primeramente el conjunto más elemental, el de los sólidos Platónicos, del cual se derivan otras categorías.

Euclides de Alejandría: Filósofo y matemático griego 325-265 A.C. que recopiló en su monumental obra: "Los Elementos" (constituída por 13 libros) el saber matemático elemental (es decir indispensable para cualquier investigación) de la civilización de su tiempo así como de los descubrimientos de las anteriores culturas: indios, asirios y egipcios, civilizaciones que precedieron a la griega. Por tanto sus libros no intentaron recopilar todo el laber de su época como erróneamente se ha afirmado, sino que su mismo título lo indica: es un conocimiento de lo elemental, lo básico para cualquier filósofo o profesional de su época: Los elementos básicos de matemática y geometría. Euclides no fue sólo un recopilador, sino que aportó gran cantidad de descubrimientos propios, como la así llamada con posterioridad 'geometría euclidiana'.

Los Elementos ha sido impreso en más de mil ediciones, es el libro no religioso con mayor tiraje en la historia y es probablemente la obra de matemática más importante, la huella de su influencia se mide en continentes, generaciones enteras, civilizaciones. Fue libro de texto en Europa hasta fines del siglo XX. Es de resaltar la claridad con la que se plantean los problemas y el rigor lógico con el que son demostrados, pues aplicó los instrumentos de lógica desarrollados por Aristóteles unas pocas décadas antes. Los seis primeros libros tratan sobre geometría en el plano, del 7 al 9 tratan sobre teoría de números, el libro 10 sobre números irracionales, y del 11 al 13 de geometría del volumen (geometría tridimensional).